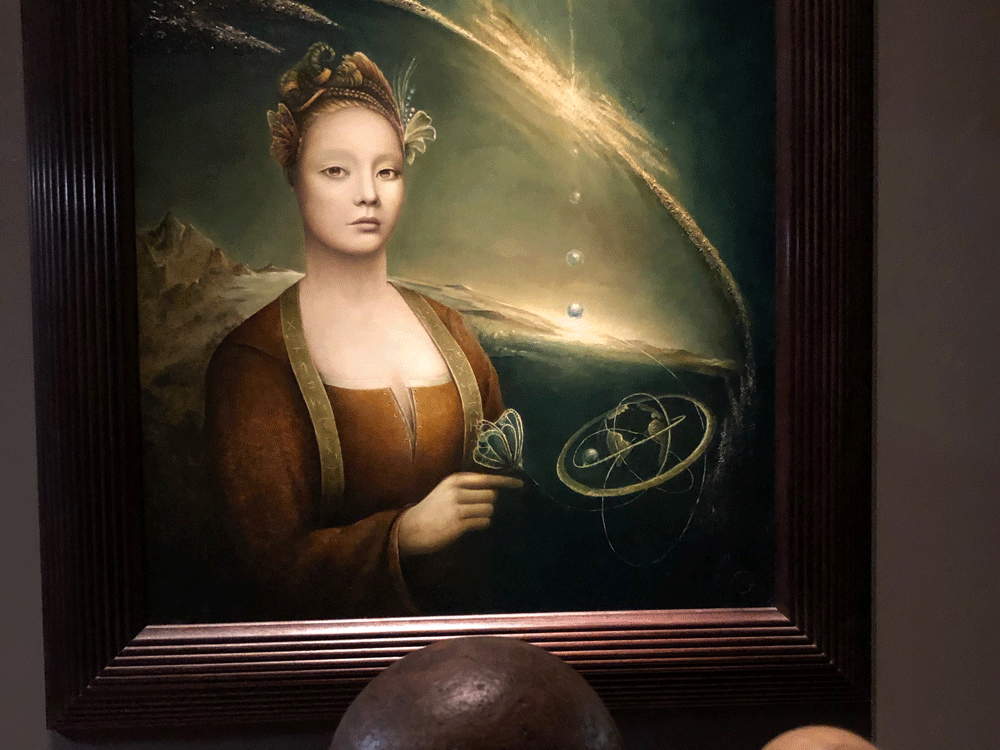"Goddess of the Universe"


"As above, so below. As within, so without"

"As above, so below. As within, so without"

"As above, so below. As within, so without"

"As above, so below. As within, so without"
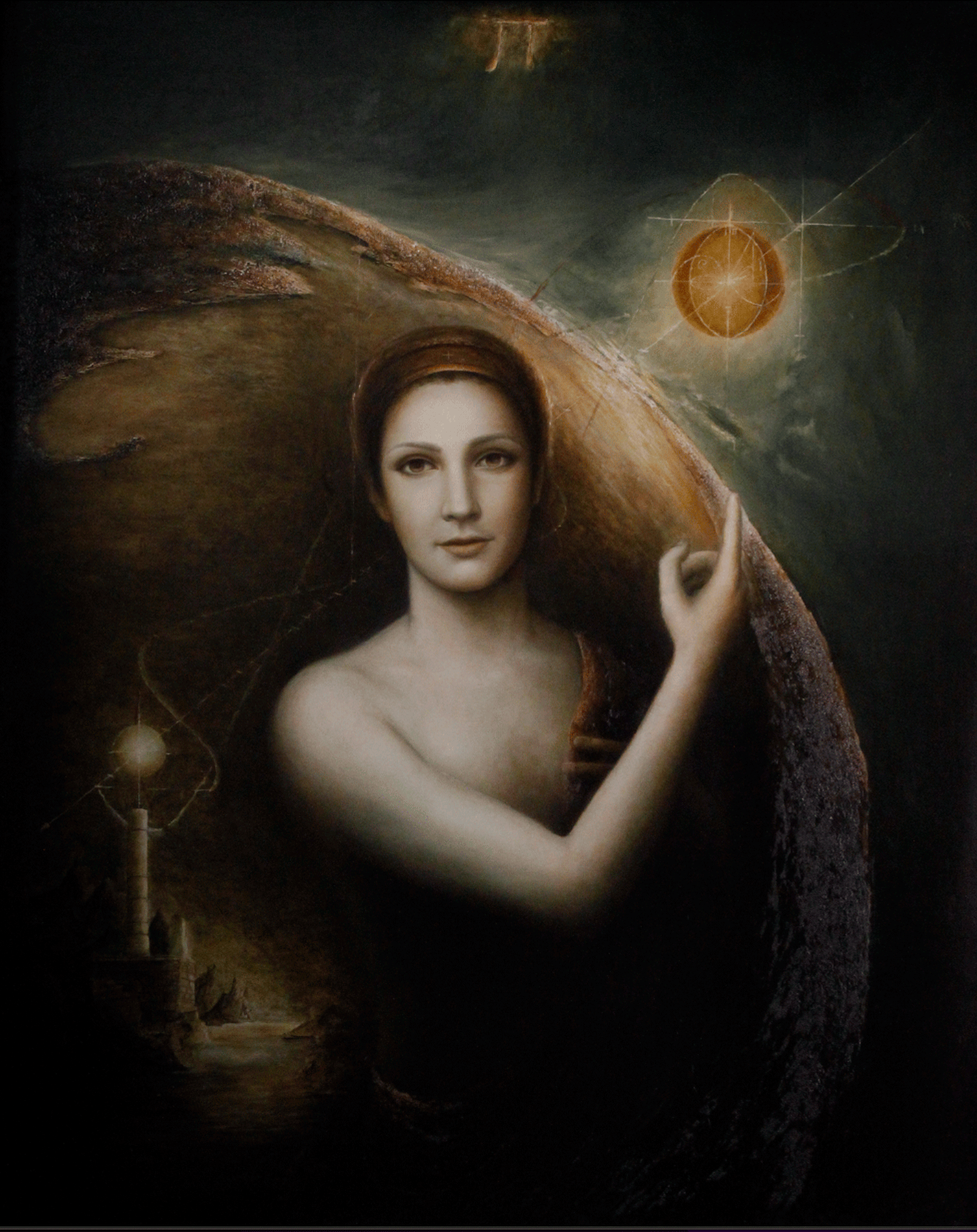
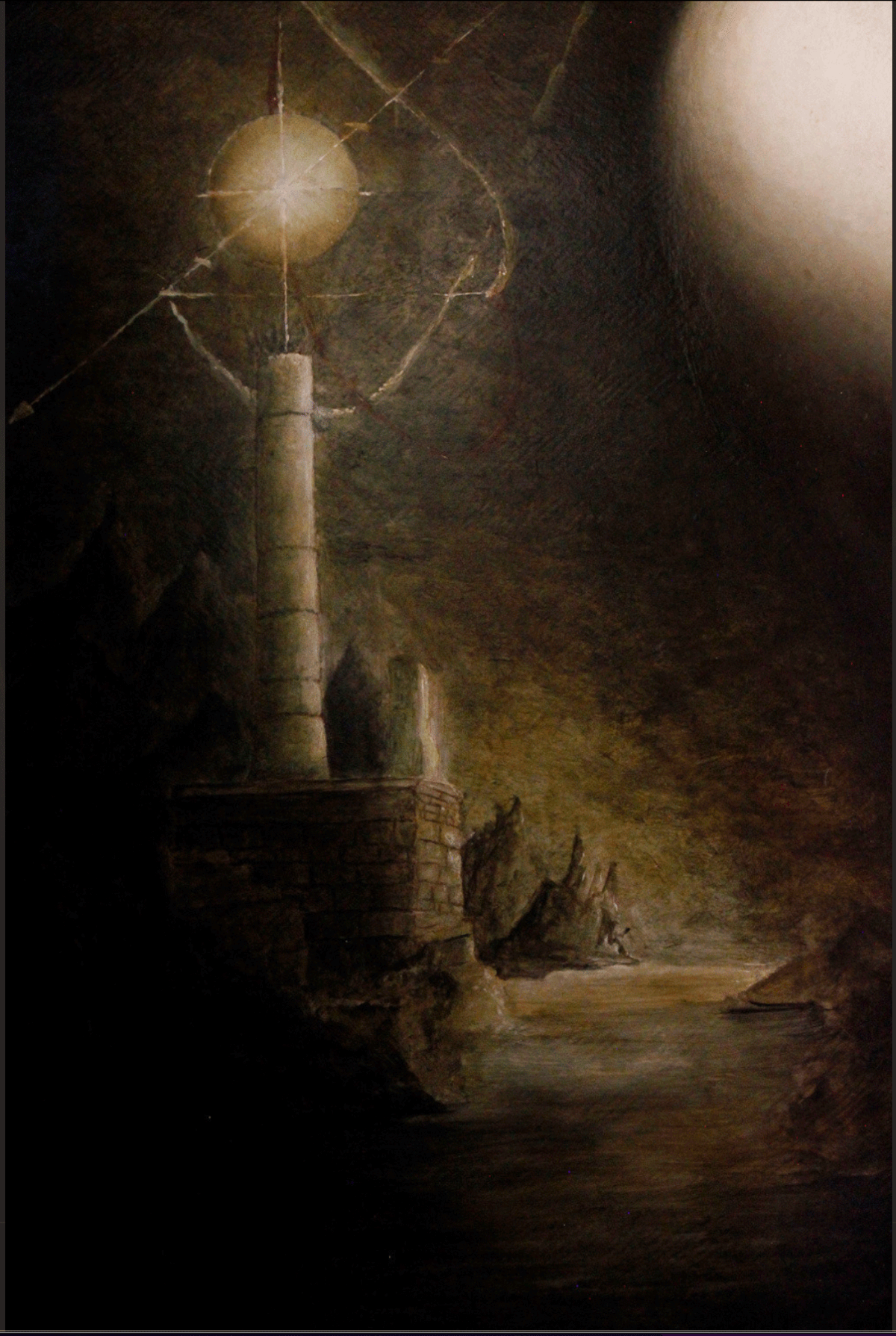

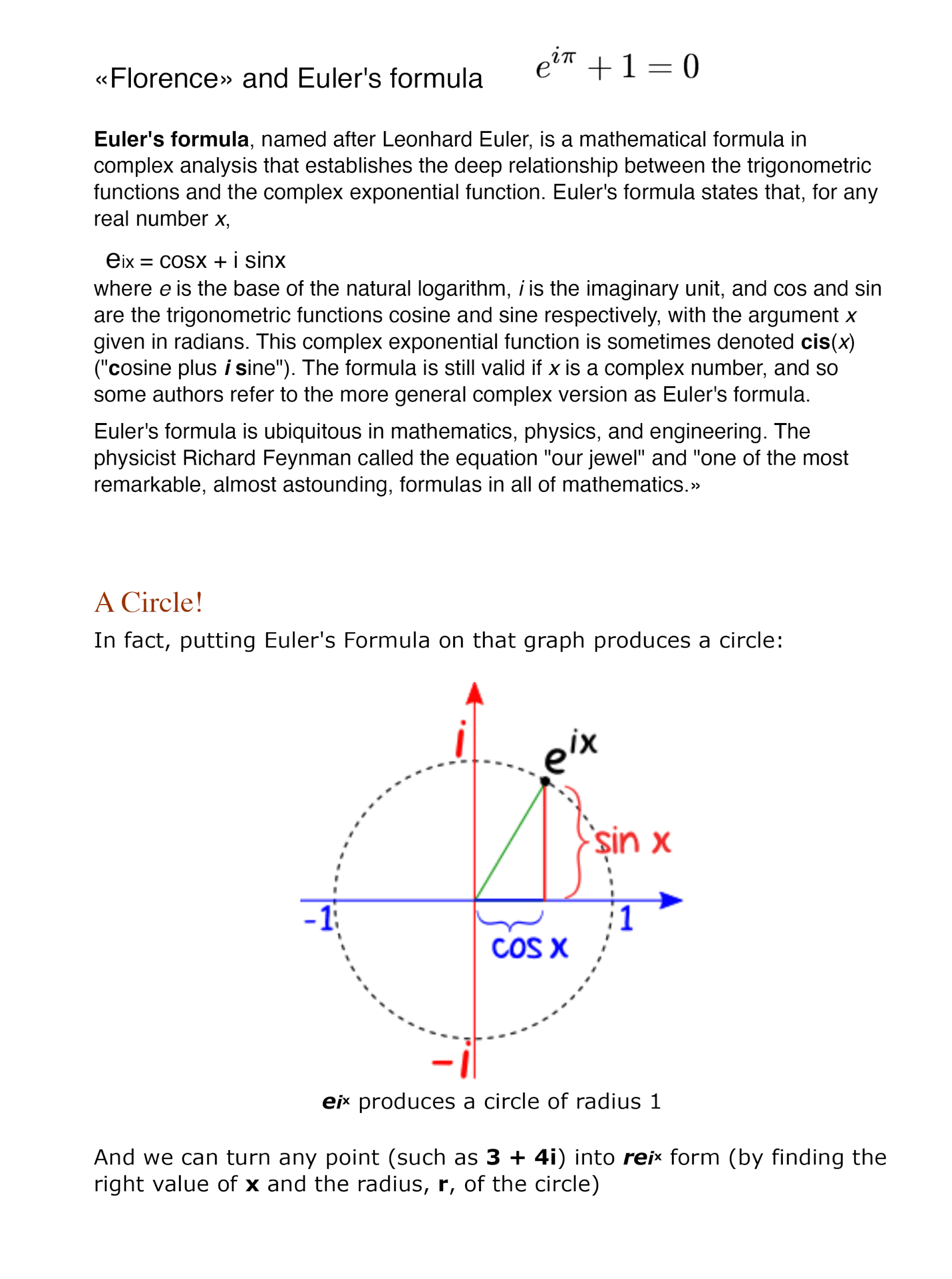
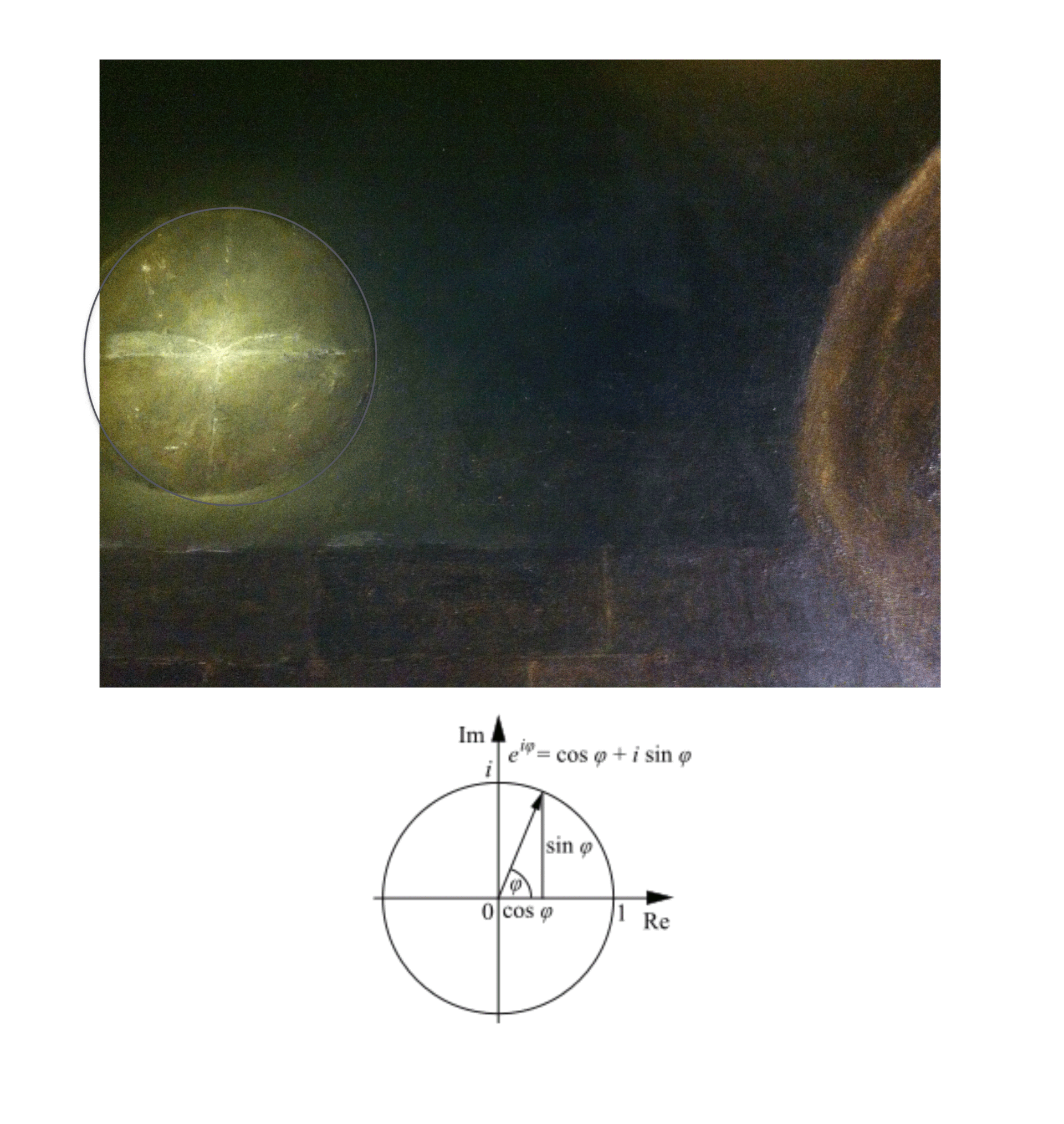



"Florence" Oil painting on canvas by Master Algrim

"Florence" detail and text
"Music of Primes" Oil painting on canvas. 150x180cm. Master Algrim
"Sombrero Galaxy" Oil painting on canvas, 180x150cm, Master Algrim

"New born" Oil painting on canvas 140x180cm.Master Algrim
"New born" detail